오늘의 공부

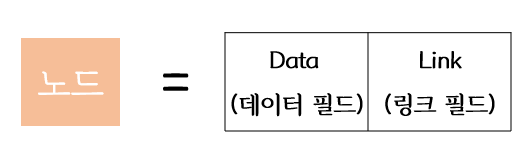
트리

Tree

트리는 객체간의 관계를 표현하는 자료구조인 그래프의 일종이다.

◎ 트리란

트리는 노드들이 가지처럼 연결된 비선형 계층적 자료구조이다.

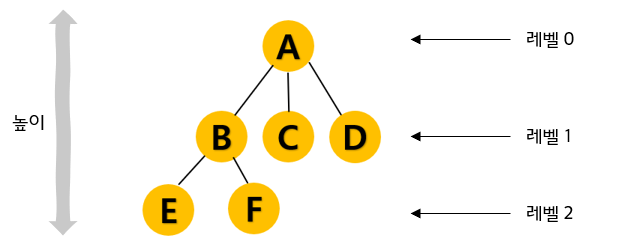
노드 : 트리의 구성요소에 해당하는 A,B, C, D, E, F와 같은 요소
간선 : 노드와 노드를 연결하는 연결선
루트 노드 : 트리 구조에서 최상위에 존재하는 A와 같은 노드
단말 노드 : 아래로 또 다른 노드가 연결되어 있지 않은 가장 마지막 (E,F,C,D와 같은) 노드
내부 노드 : 단말 노드를 제외한 모든 노드
레벨 : 각 층 별로 숫자를 매긴 것
높이 : 트리의 최고 레벨

◎ 이진트리

이진트리란 루트 노드를 중심으로 두 개의 서브 트리로 나누어지며 나누어진 두 서브 트리도 모두 이진 트리여야 한다.
즉, A를 기준으로 B,D,E가 왼쪽 서브 트리 C,F,G가 오른쪽 서브트리이며 각각의 서브 트리들도 이진 트리여야 한다.

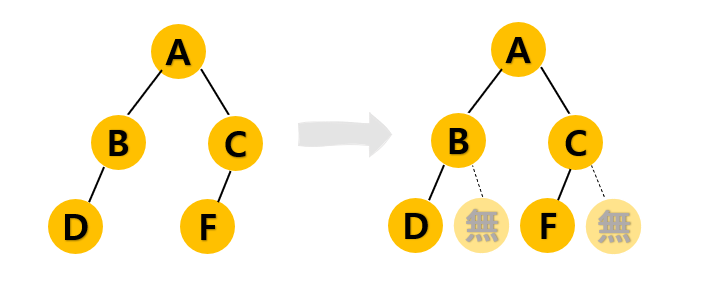
여기서 왼쪽과 같은 트리도 이진트리가 된다.
노드가 위치할 수 있는 곳에 노드가 존재하지 않으면 공집합 노드가 존재하는 것으로 간주해 공집합 노드도 '노드로 인정'하기 때문이다.

이진 트리는 여러 분류로 나뉠 수 있는데 그 중 완전 이진트리와 포화 이진트리가 존재한다.

포화 이진 트리는 위의 그림과 같이 모든 레벨이 꽉 차 있으며 노드를 더 추가하려면 레벨을 늘려야 하는 트리이다.

이 포화 이진 트리에서 레벨을 하나 더 늘려 H와 I를 추가한 다음 이진 트리를 보면 포화 이진 트리처럼 모든 레벨이 꽉 찬 상태는 아니지만 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리가 된다.
여기서의 '차곡차곡 빈 틈 없이'는 노드가 위에서 아래로, 그리고 왼쪽에서 오른쪽의 순서대로 채워졌다는 의미가 된다.
이 트리가 바로 완전 이진 트리이다.

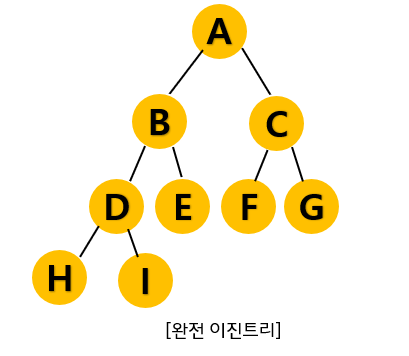
완전 이진트리는 임의의 두 단말 노드의 레벨 차이가 1이하인 경우이며 위의 그림과 같이 왼쪽에서 오른쪽으로 채워진 이진트리를 뜻한다.
레벨 n까지의 모든 노드수는 2^n -1개이다.

◎ 트리의 순회

트리의 순회란 트리에 속하는 모든 노드를 한 번씩 방문하는 것이다. 트리의 순회 방식에는 전위, 중위, 후위 방식이 있다.
루트를 방문하는 작업을 V, 왼쪽과 오른쪽 서브 트리를 방문하는 작업을 각각 L과 R이라고 하면
전위는 VLR, 중위는 LVR, 후위는 LRV 이다.

트리의 순회는 쉬워보이지만 복잡한 노드의 트리인 경우 생각보다 헷갈리게 된다.

다음과 같은 사진이 있을 때 전위, 중위, 후위 순회의 결과는 다음과 같다.
전위 순회 : F,B,A,D,C,E,G,I,H
중위 순회 : A,B,C,D,E,F,G,H,I
후위 순회 : A,C,E,D,B,H,I,G,F

전위 순회

Void preorder(TNode *n) 
{ 
	If( n!= NULL ) 
    { 
    	Printf(“[%c]”, n->data); 
        Preorder(n->left); 
        Preorder(n->right); 
     }
}

중위 순회

Void inorder(TNode *n) 
{ 
	If( n!= NULL ) 
	{ 
    	inorder(n->left); 
        Printf(“[%c]”, n->data); 
        inorder (n->right); 
    } 
}

후위 순회

Void postorder(TNode *n) 
{ 
	If( n!= NULL ) 
	{ 
    	postorder(n->left); 
        postorder (n->right); 
        Printf(“[%c]”, n->data); 
    } 
}

참고로 이 트리의 전위순회 방식을 일반화시킨 그래프의 정점 순회 방법이 깊이 우선탐색 (DFS)이다.
탐색 도중에 인접된 모든 정점이 이미 방문된 정점을 만났을 때 바로 이전에 방문한 정점으로 돌아가기 위해 스택을 사용한다.



참고 자료;
윤성우의 열혈 자료구조 (저; 윤성우, 출판; 오렌지 미디어)

https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EC%88%9C%ED%9A%8C

스택 C언어로 구현하기 (배열)

Stack 

먼저 들어온 데이터가 나중에 나가는 구조를 가지고 있는 스택은 배열과 연결리스트로 구현할 수 있다.

그 중 배열을 이용한 구현 방법은 다음과 같다. 

◎ 배열

배열을 스택으로 구현하기 위해 기억해야 할 것은 두 가지이다.

처음 인덱스 0의 배열 요소를 스택의 바닥(Bottom)으로 정의하고 마지막에 저장된 데이터의 위치를 기억해야 한다.

인덱스 0의 요소를 스택의 Bottom으로 정의하면 배열의 길이와 관계없이 항상 인덱스 0의 요소가 스택의 Bottom이 되며 마지막에 저장된 데이터의 위치는 Top이 되기 때문이다. 

◎ 삽입(Push)과 삭제(Pop)

삽입, 즉 Push는 Top Index를 위로 한 칸 올리고 Top이 가리키는 배열의 위치에 해당 데이터를 저장한다.

삭제 Pop은 Top Index의 데이터를 반환하고 Top Index를 한 칸 줄인다. 

void push(int num)
{
	stack[++index] = num;
}

int pop()
{
	return stack[index--];
}

참고 자료;

윤성우의 열혈 자료 구조 (출판사; 오렌지 미디어, 저: 윤성우)

스택  C언어로 구현하기 (연결리스트)

Stack!

먼저 들어온 데이터가 나중에 나가는 구조를 가지고 있는 스택은 배열과 연결리스트로 구현할 수 있다.

그 중 연결리스트의 구현 방법은 다음과 같다. 

◎ 연결리스트

배열을 이용한 것과 달리 연결 리스트로 구현한 스택에서는 요소들을 한꺼번에 할당하는 것이 아니다.

동적 할당을 이용해서 필요할 때마다 하나씩 할당하는 방식을 이용한다. 

연결리스트로 구현하기 위한 스택은 아래와 같은 노드 구조체를 추가로 정의해야 한다.

이 때 스택에 저장할 정보(데이터 필드)와 함께 다음 노드를 가리키기 위한 포인터(링크 필드)를 멤버로 가진다.

typedef struct LinkedNode
{
	int data; // 데이터 필드
	struct LinkedNode* link // 링크 필드(포인터) -> 다음 노드를 가리킴
 } Node; 

배열에서는 top(제일 위의 값)을 index값으로 저장했지만 연결리스트에서는 포인터로 저장해야 한다.

즉 헤드포인터를 저장하는 것이다.

헤드 포인터가 이해가 안된다면 ?

○삽입

만약 C->B->A 순으로 연결되어 있다면 헤드 포인터 top은 C를 가리키고 있고 C의 링크 필드가 B를 B의 링크 필드가 A를 가리키고 있을 것이다. 

여기에 새로운 노드 D를 삽입하려고 하면 성공했을 경우 top은 D의 노드를 가리키고 D는 C를 가리켜야 한다.

(왜? 스택의 특성상 먼저 들어온 값이 앞, 또는 위에 있기 때문에) 

1. 노드 D의 링크 필드가 노드 C를 가리키도록 함 p->link = top;

2. 헤더 포인터 top이 노드 D를 가리키도록 함 top = p;

이 두 가지의 과정을 거치면 push를 구현할 수 있다. 

void push(int e)
{
	Node* p = (Node*)malloc(sizeof(Node));
 	p->data = e;   // 데이터를 초기화
    
	p->link = top; // 1번
	top = p;   // 2번
 } 

○삭제

삭제 연산은 가장 최근에 삽입된 요소를 꺼내서 반환하는 연산이다.

스택은 FIFO, 즉 First in First Out인 큐와 달리 FILO(First in Last Out)이므로 삭제 시에 가장 최근에 삽입된 요소를 꺼내게 된다. 

1. 포인터 변수 p가 노드 C를 가리키도록 함 p = top

2. 헤더 포인터 top이 다음 노드를 가리키도록 함 top = p->next 

이 연산을 구현할 때 신경써야 할 부분은 메모리를 동적으로 해제하는 것이다.

항목을 반환하기 위해서 해제 하기 전에는 데이터 필드를 저장해두고 노드를 해제한 후에 저장된 항목을 반환해야 한다. 

int pop()
{
	Node* p;
	int e;
	if(is_empty())   // 스택이 비었는지 확인 -> 비었으면 pop할 데이터 X
    	error("스택 공백 에러");

	p = top;
	top = p->link;
	e = p->data;
	free(p); // 노드 동적 해제하기
	return e; // 반환
} 

참고 자료;

두근두근 자료구조 (출판사; 생능출판, 저;최영규, 천인국, 공용해)

연결리스트

Linked-List

연결리스트는 말 그대로 연결된 리스트이다. 물리적으로 흩어져 있는 자료들을 서로 연결해 하나로 묶는 방법인 것이다.

배열을 이용한 자료구조는 구현이 간단하지만 용량이 고정된다는 단점이 있다. 배열은 동적으로 크기를 늘리거나 줄일 수 없어서 처음 할당한 공간이 가득 차면 더 이상 데이터를 추가할 수 없기 때문이다.

그렇다면 연결리스트는? 데이터와 링크로 구성돼 있고 링크가 노드들을 연결하는 역할을 한다. 따라서 노드들의 연결만 바꿔주면 되니까 용량이 자동으로 변할 수 있는 것이다. 

그래서 배열에 비해 중간에 자료를 삽입하는 것이 용이하고 크기가 고정되지 않는다. 

배열에서 어떤 자료를 추가하고자 할 때는 그 위치 이후의 자료를 한 칸씩 뒤로 복사해 넣어주고 그 자리에 자료를 넣어줘야 한다.

하지만 연결 리스트에는 이럴 필요가 없다.

왜? 

◎ 삽입과 삭제 

위와 같이 노드들이 연결되어 있다고 할 때 (A->B->C->D->E) 데이터를 삽입하고자 한다. 

B와 C사이에 N을 삽입하려고 한다면? 

이렇게 B와 C를 연결해 주던 것을 없애고 B를 N과 N과 C를 연결한다. 그러면 A->B->N->C->D->E 순으로 연결되며 B와 C사이에 N이 위치하게 된다. 

삭제도 마찬가지이다. 

C를 없애고 싶다면 C로 연결되던 B와 D의 선을 지우고 B와 D를 연결시켜 주면 된다. 

◎ 연결리스트의 구조

연결리스트의 구조에는 크게 두 가지 노드와 헤드포인터가 있다.

○ 노드 (node)

위의 그림에서 A,B,C,D,E에 해당하는 것들이 노드이다. 연결리스트는 노드들의 집합이고 이들은 데이터를 저장하고 있으며 서로 연결되어 있다.

이 노드는 데이터를 담는 데이터 필드와 링크를 담는 링크 필드로 구성되어 있다.

데이터 필드에는 말 그대로 데이터가 들어간다. 담고 싶은 정보를 담는 곳이다. 정수가 될 수 있고 구조체가 될 수도 있다. 

링크 필드에는 다른 노드를 가리키는 정보가 들어있다. 위 사진에서는 화살표에 해당하며 다른 노드의 주소를 저장하는 포인터 변수가 존재한다. 이 포인터를 이용해서 현재 노드에 연결되어 있는 다음 노드가 어떤 노드인지 알 수 있는 것이다. 

○헤드 포인터(head pointer)

헤드 포인터는 연결 리스트의 첫 번째 노드의 주소를 저장하는 포인터이다. 

연결 리스트는 첫 번째 노드를 알면 그 뒤에 매달려 있는 모든 노드들에 순차적으로 접근할 수 있다.

그래서 헤드 포인터 주소를 반드시 알아야 한다. 

(마지막 노드 같은 경우에는 더 이상 연결할 노드가 없는데 링크 필드의 값을 NULL로 설정해서 이 노드가 마지막 노드임을 표현한다.)

◎ 연결리스트의 특징 

- 노드들은 메모리의 어느 곳에나 위치할 수 있다.

즉, 노드들의 주소가 연결 리스트 상의 순서와 동일하지 않다. 인접한 노드라고 해서 인접한 메모리에 있는 것이 아니다.

- 연속적인 기억공간이 없어도 데이터를 저장하는 것이 가능하고 미리 공간을 확보할 필요도 없다. 필요할 때마다 동적으로 노드를 생성해서 연결하기 때문이다.

- 링크 필드를 위한 추가 공간이 필요하다.

- 연산의 구현이나 사용 방법이 배열에 비해 복잡하다.

- 오류가 없더라도 동적 할당과 해제가 너무 빈번하게 일어나면 메모리 관리를 위한 처리시간이 길어져 프로그램이 느려질 수도 있다. 

◎ 연결리스트의 종류

연결리스트는 연결의 종류에 따라 세 가지로 나뉜다.

1. 단순 연결 리스트

하나의 방향으로만 연결되어 있으며, 맨 마지막 녿의 링크 필드는 NULL 값을 가진다.

2. 원형 연결 리스트

단순 연결 리스트와 같지만 맨 마지막 노드의 링크 값이 다시 첫 번째 노드를 가리킨다. 그래서 원형으로 연결 되었다고 표현하는 것이다.

3. 이중 연결 리스트

각 노드마다 링크 필드, 즉 포인터가 2개씩 존재한다. 따라서 각각의 노드는 선행 노드와 후속 노드를 모두 가리킬 수 있다. 

참고 자료;

두근두근 자료구조 (출판사; 생능 출판 / 저 ;최영국, 천인국, 공용해 )

트라이(Trie)

트리구조의 트라이

트라이(trie)는 탐색 트리의 일종으로 동적 집합이나 연관 배열을 저장하는데 사용하는 자료구조이다. 알고리즘 문제 등에서는 주로 문자열 저장 문제의 해결 방법으로 종종 등장한다.

문자열 검색을 빠르게 해주는 이진 탐색 트리의 구조로 한 레벨당 문자가 하나씩 저장되므로 문자열 검색 시 시간 복잡도는 O(NlogN)이다. 

위의 사진은 "A", "to", "tea", "ted", "ten", "i", "in", "inn"를 키로 둔 트라이.

◎ 알고리즘

트라이는 탐색과 삽입을 지원하는 노드로 구성된 트리이다. 

주어진 문자열을 이루고 있는 문자를 앞에서 부터 하나씩 노드를 생성해가며 만들어진다. 

탐색의 순서는 다음과 같다.

1. 탐색하려고 하는 문자열을 가져와 첫 번째 문자가 저장되어 있는지 체크한다. 

2. 현재 문자로 이루어진 노드가 존재하면 그 노드로 그 다음 문자열을 탐색하고 노드가 없으면 그 노드를 새로 할당받은 후, 해당 노드를 통해 다음 문자열을 탐색한다.

3. 문자열의 마지막이 될 때까지 위의 과정을 반복한다. 

참고 자료;

URL

ko.wikipedia.org/wiki/%ED%8A%B8%EB%9D%BC%EC%9D%B4_(%EC%BB%B4%ED%93%A8%ED%8C%85)