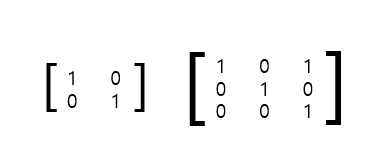행렬 上
행렬과 단위행렬, 전치
◎ 행렬
m x n 행렬 M은 m개의 행과 n개의 열로 이루어진 실수들의 정사각 배열이다.
행(row)들의 개수와 열(column)들의 개수를 곱한 것을 행렬의 차원이라고 부르고 행렬을 구성하는 수들을 원소(element) 도는 성분(entry)라고 부른다.
 A는 행이 3, 열이 3인 3x3 행렬이다.
A는 행이 3, 열이 3인 3x3 행렬이다.
종종 한 행렬의 행들을 벡터로 간주하는 것이 편할 때가 있다. 예를 들면 A 행렬의 A1* 는 A11, A12, A13으로 하나의 행벡터를 뜻하게 된다. 이 때 *는 하나의 행벡터 전체를 뜻하게 된다.
열벡터도 마찬가지로 A*1는 A11, A21, A31을 뜻하며 여기서의 *는 하나의 열벡터 전체를 뜻한다.
행렬의 한 성분을 지칭할 때에는 그 성분의 행과 열 번호를 이중 아래첨자(색인)로 지정하는 형태의 표기법을 사용한다.
 여기서 첫 아래첨자 i가 행, 둘째 아래첨자 j가 열
여기서 첫 아래첨자 i가 행, 둘째 아래첨자 j가 열
◎ 행렬의 연산
행렬의 상등, 덧셈, 스칼라 곱셈, 뺄셈을 정의해 보면
1. 두 행렬은 오직 대응되는 성분들이 상등일 때에만 상등이다. 따라서, 두 행렬의 상등을 비교하려면 두 행렬의 행 수와 열 수가 동일해야 한다.
2. 두 행렬을 더할 때에는 대응되는 성분들을 더한다. 따라서 행 수와 열 수가 같은 행렬들만 덧셈이 가능하다.
3. 행렬에 하나의 스칼라를 곱할 때는 행렬의 모든 성분에 그 스칼라를 곱한다.
4. 행렬의 뺄셈은 스칼라 곱셈과 행렬 덧셈으로 정의한다. 즉, A - B = A + (-1 x B) = A + (-B)이다.
덧셈과 스칼라 곱셈이 성분별로 이루어지기 때문에 행렬의 덧셈과 스칼라 곱셈도 실수의 덧셈 및 곱셈의 다음과 같은 속성들을 만족한다.
| A + B = B + A |
덧셈의 교환법칙 |
| ( A + B ) + C = A + ( B + C ) |
덧셈의 결합법칙 |
| r ( A + B ) = rA + rB |
행렬들에 대한 스칼라의 분배법칙 |
| ( r + s ) A = rA + sA |
스칼라들에 대한 행렬의 분배법칙 |
◑ 행렬의 곱셈
위에서 덧셈은 행렬의 열 수와 행 수가 동일해야 했는데 곱셈은 조금 다르다.
교환법칙이 성립하지 않는 행렬의 곱셈은 앞의 행렬의 열과 뒤에 곱할 행렬의 행의 수가 같아야 한다.
즉, A(앞에 곱하는 행렬)의 행벡터 차원과 B(뒤에 곱하는 행렬)의 열벡터 차원을 일치시켜야 한다.
만일 A가 m x n 행렬이고 B가 n x p 행렬이면 둘의 곱 AB가 정의된다. 곱 AB는 하나의 m x p 행렬이 된다.
행렬 A와 B를 곱한 결과가 C라고 할 때 C의 ij번째 성분은 A의 i번째 행벡터와 B의 j번째 열벡터의 내적이 된다.
 2x2 행렬과 2x3 행렬을 곱해서 2x3 행렬이 나왔다.
2x2 행렬과 2x3 행렬을 곱해서 2x3 행렬이 나왔다.
◑ 행렬의 전치
행렬의 전치, 즉 전치행렬은 주어진 행렬의 행들과 열들을 맞바꾼 것을 말한다.
따라서 m x n 행렬의 전치는 n x m 행렬이다.
행렬 M의 전치행렬은 다음과 같이 표기한다.


◑ 단위행렬
행렬에는 단위행렬이라고 부르는 특별한 행렬이 있다. 주대각 성분, 즉 좌상에서 우하로의 주된 대각선에 있는 성분들만 1이고 나머지는 모두 0인 정방행렬(정사각형 행렬, 즉 열 수와 행 수가 같은 행렬)이다.
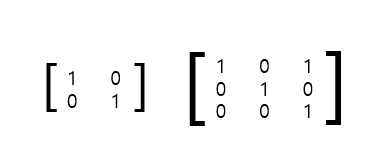 2x2와 3x3 의 단위행렬
2x2와 3x3 의 단위행렬
이 단위행렬은 곱셈의 항등원 역할을 한다.
항등원?
더보기
연산(演算)에서 임의의 원소 a에 대하여 ae=ea=a를 만족하는 원소 e를 가리키는 말. 이를테면, a+0=a, a·1=a이므로 이 때 0을 덧셈의 항등원, 1을 곱셈의 항등원이라 함.
즉, 만일 A가 m x n 행렬이고 B가 n x p 행렬 그리고 I 가 n x n 행렬이면 AI = A, IB = B.
그러니까 어떤 행렬에 단위행렬을 곱해도 그 행렬은 변하지 않는다.
곱할 행렬 M이 정방행렬이라면 단위행렬과의 곱셈은 교환법칙을 만족한다.
참고 자료;
- Direct11을 이용한 3D게임프로그래밍 (저; 프랭크 D. 루나, 역; 류광, 출판사; 한빛미디어)