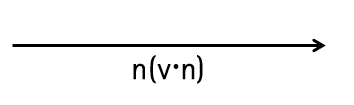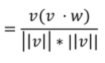오늘의 공부

슬라이딩 벡터

Sliding Vector

슬라이딩 벡터는 충돌 시에 입사벡터가 입사면을 따라서 미끄러지게 하기 위해서 수평 성분만을 남긴 벡터이다. 

구하는 방법에는 반사벡터를 이용해 구하는 방법과 일반적인 방법이 있다.

◎ 반사 벡터를 이용해서 구하는 방법

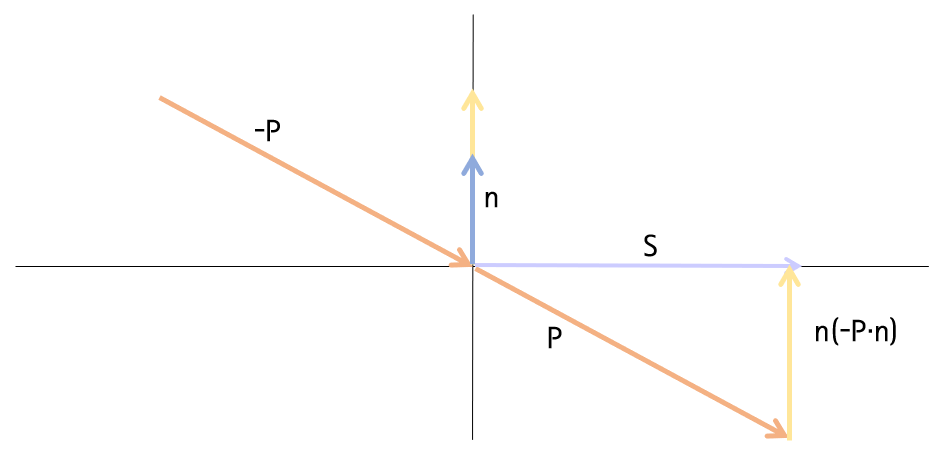
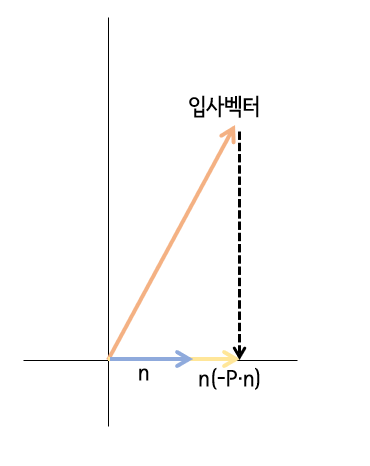
반사 벡터에서 입사벡터 P에 n(-P·n)을 한번 더해주면 입사면에 투영된 접선벡터를 구할 수 있다.

입사벡터의 역벡터 -P가 n에 투영된 n(-P·n)을 이용해 슬라이딩 벡터를 구하고 있는 중이다.

따라서 반사 벡터를 이용할 때 슬라이딩 벡터 S를 구하는 공식은 다음과 같다. 

S = P + n(-P·n)

◎ 일반적인 방법

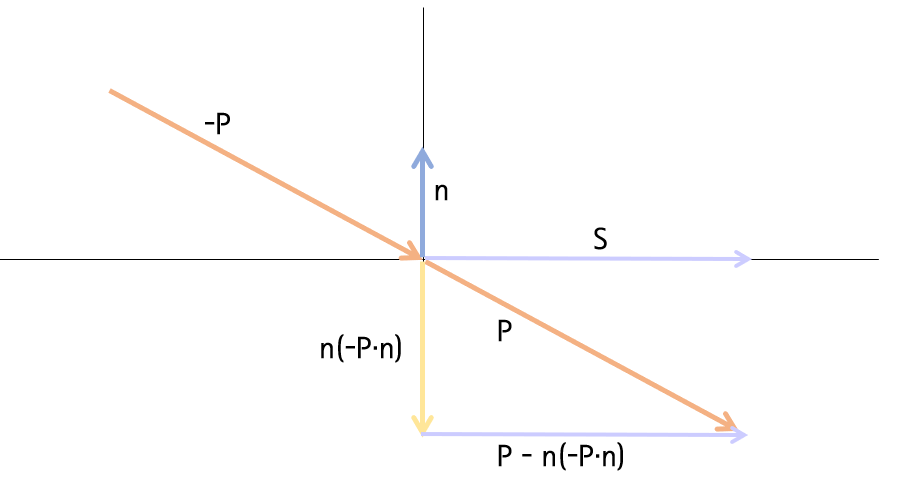
일반적인 방법으로는 입사벡터 P를 n에 바로 투영시킨다.

입사벡터 P와 법선벡터 n의 끼인 각이 0≤ θ ≤ π/2 일 때, P·n의 값은 음수가 되므로, n벡터의 역벡터 방향으로 투영 벡터가 생성된다.

이렇게 얻을 수 있는 투영벡터 n(-P·n)을 입사벡터 P에서 빼주면 슬라이딩 벡터 S를 얻을 수 있다.

이때의 슬라이딩 벡터 S를 구하는 공식은 다음과 같다.

S = P - n(-P·n)

참고 자료;

https://toymaker.tistory.com/entry/%EB%AF%B8%EB%81%84%EB%9F%AC%EC%A7%90-%EB%B2%A1%ED%84%B0-Sliding-Vector?category=500302 

반사벡터

Reflection Vector

반사 벡터는 정반사이다.

정반사는 입사각과 반사각이 동일한 반사를 의미한다. 

◎ 투영 벡터

반사 벡터를 구하려면 투영 벡터를 먼저 구해야 한다.

투영이란 어떤 벡터 v를 단위 벡터 n에 내적하여 구할 수 있는 v의 n방향으로의 길이를 뜻한다. 

내적값이 스칼라이므로 투영된 방향으로의 벡터를 구하려면 이 내적값에 방향벡터 n을 곱해주면 된다. 

(v·n)n을 이용해 벡터를 구할 수 있게 된다. 

* 왜 이렇게 되는지 추가 설명!

더보기

v와 n을 내적하면 cosθ를 결과값으로 얻게 된다.

v·n = ||v||||n||cosθ

 

여기서 이 삼각형은 직각삼각형이므로 코사인값은 밑변/빗변 즉, ||n|| / ||v|| 이다.

||n|| = ||v||cosθ 이고 투영한 길이를 w라고 했을 때

w = ||v||cosθ가 된다. 

 

길이를 구했으니 방향도 알아야 하는데, 길이가 1인 단위벡터는 방향의 정보만을 갖고 있으므로 

단위벡터인 n의 방향으로의 길이를 구하려는 투영의 값에 n을 곱해주면 된다.

 

n의 방향 벡터 = n / ||n||

투영 벡터 = ( n / ||n|| ) * ||v||cosθ

 

하지만 두 벡터 사이각을 항상 알 수 없으므로

v·n = ||v||||n||cosθ 라는 사실을 응용해서 v·n/||n|| = ||v||cosθ 이런식을 만들어내면

두 벡터만 주어졌을 때, 한 벡터를 다른 벡터에 투영하는 공식을 구했을 때

((v·n) / ||n|| ) * ( n / ||n|| ) 이런 공식이 나오게 된다.

 

◎ 반사벡터 

투영 벡터를 이용해 구한 벡터로 반사 벡터를 계산한다.

다음과 같이 입사벡터(P)와 법선 벡터(n)이 있을 때 반사 벡터(R)은 입사벡터(P)와 크기가 같고 반사각과 입사각이 같다.

P와 n을 이용하면 반사벡터(R)을 구할 수 있다. 

우선 위의 투영 벡터를 구하는 방식을 이용해 입사 벡터 P의 역벡터 -P를 n의 연장선상에 투영시켜서 투영벡터 n(-P · n)을 구한다. 

어떻게 투영 벡터를 구하는건지? 

더보기

이렇게 돌려보면 쉽게 알 수 있다!

그 후 입사 벡터 P의 시작 위치를 원점에 위치 시키고 투영으로 구한 n(-P·n)를 더하면 입사면에 투영된 벡터의 위치를 구할 수 있다. 

입사 벡터 P에 n(-P·n)를 한 번 더하면 입사면에 투영된 위치를, 두번 더하면 반사벡터 R을 구할 수 있다.

따라서 반사벡터 R을 구하는 공식은 다음과 같다.

R = P + 2n(-P·n)

참고 자료;

https://toymaker.tistory.com/entry/%EB%B0%98%EC%82%AC-%EB%B2%A1%ED%84%B0-Reflection-Vector

https://ifyouwanna.tistory.com/entry/%EB%B0%98%EC%82%AC%EB%B2%A1%ED%84%B0

https://gyong0.tistory.com/22

두 점 사이의 거리 구하기

2차원과 3차원

플레이어 사이의 거리 혹은 충돌하려는 두 물체 사이의 거리, 더 나아가서는 사정 거리 안에 들어왔는지 아닌지를 알고 싶을 때가 생기면 어떻게 해야 할까?

가장 간단한 방법은 피타고라스의 정리를 이용하는 것이다.

◎ 두 점 사이의 거리

A와 B를 잇는 선분을 하나 그린 후 이를 빗변으로 하는 직각 삼각형을 하나 그린다.

A(x1, y1), B(x2, y2)라 할 때 나머지 하나의 꼭짓점의 좌표는 C(x2, y1)이 된다. 

여기서 피타고라스의 정리를 사용하면 A와 B를 잇는 빗변의 거리를 구할 수 있다.

제곱근은 직접 연산을 통해 계산해도 되지만 <math.h> 헤더를 추가해 sqrt 와 pow를 이용해도 된다. 

sqrt(값) 제곱근을 구하는 함수로 제곱근을 반환 

pow(값, 지수) 제곱을 구하는 함수. 

◎ 3차원으로의 확장

위의 거리의 공식은 xy축에 추가로 z축을 사용하는 3차원으로도 쉽게 확장할 수 있다.

공식에 z좌표만 추가하면 된다.

두 점 A(x1, y1, z1), B(x2, y2, z2) 사이의 거리는