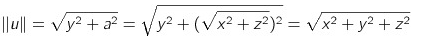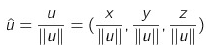오늘의 공부

반사벡터

Reflection Vector

반사 벡터는 정반사이다.

정반사는 입사각과 반사각이 동일한 반사를 의미한다. 

◎ 투영 벡터

반사 벡터를 구하려면 투영 벡터를 먼저 구해야 한다.

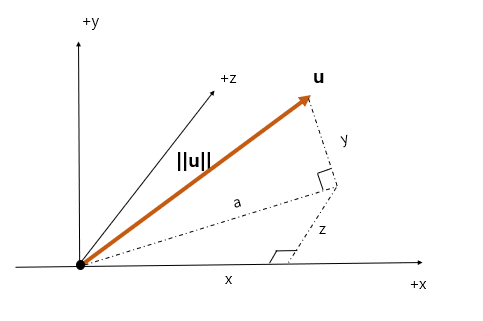
투영이란 어떤 벡터 v를 단위 벡터 n에 내적하여 구할 수 있는 v의 n방향으로의 길이를 뜻한다. 

내적값이 스칼라이므로 투영된 방향으로의 벡터를 구하려면 이 내적값에 방향벡터 n을 곱해주면 된다. 

(v·n)n을 이용해 벡터를 구할 수 있게 된다. 

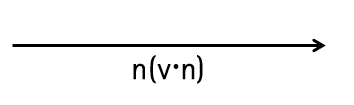
* 왜 이렇게 되는지 추가 설명!

더보기

v와 n을 내적하면 cosθ를 결과값으로 얻게 된다.

v·n = ||v||||n||cosθ

 

여기서 이 삼각형은 직각삼각형이므로 코사인값은 밑변/빗변 즉, ||n|| / ||v|| 이다.

||n|| = ||v||cosθ 이고 투영한 길이를 w라고 했을 때

w = ||v||cosθ가 된다. 

 

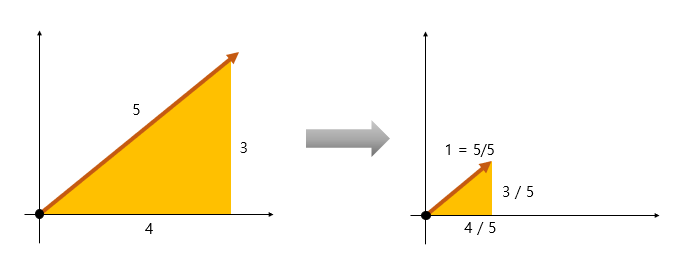
길이를 구했으니 방향도 알아야 하는데, 길이가 1인 단위벡터는 방향의 정보만을 갖고 있으므로 

단위벡터인 n의 방향으로의 길이를 구하려는 투영의 값에 n을 곱해주면 된다.

 

n의 방향 벡터 = n / ||n||

투영 벡터 = ( n / ||n|| ) * ||v||cosθ

 

하지만 두 벡터 사이각을 항상 알 수 없으므로

v·n = ||v||||n||cosθ 라는 사실을 응용해서 v·n/||n|| = ||v||cosθ 이런식을 만들어내면

두 벡터만 주어졌을 때, 한 벡터를 다른 벡터에 투영하는 공식을 구했을 때

((v·n) / ||n|| ) * ( n / ||n|| ) 이런 공식이 나오게 된다.

 

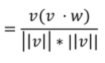
◎ 반사벡터 

투영 벡터를 이용해 구한 벡터로 반사 벡터를 계산한다.

다음과 같이 입사벡터(P)와 법선 벡터(n)이 있을 때 반사 벡터(R)은 입사벡터(P)와 크기가 같고 반사각과 입사각이 같다.

P와 n을 이용하면 반사벡터(R)을 구할 수 있다. 

우선 위의 투영 벡터를 구하는 방식을 이용해 입사 벡터 P의 역벡터 -P를 n의 연장선상에 투영시켜서 투영벡터 n(-P · n)을 구한다. 

어떻게 투영 벡터를 구하는건지? 

더보기

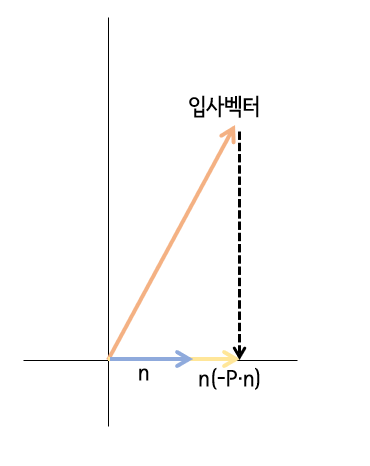
이렇게 돌려보면 쉽게 알 수 있다!

그 후 입사 벡터 P의 시작 위치를 원점에 위치 시키고 투영으로 구한 n(-P·n)를 더하면 입사면에 투영된 벡터의 위치를 구할 수 있다. 

입사 벡터 P에 n(-P·n)를 한 번 더하면 입사면에 투영된 위치를, 두번 더하면 반사벡터 R을 구할 수 있다.

따라서 반사벡터 R을 구하는 공식은 다음과 같다.

R = P + 2n(-P·n)

참고 자료;

https://toymaker.tistory.com/entry/%EB%B0%98%EC%82%AC-%EB%B2%A1%ED%84%B0-Reflection-Vector

https://ifyouwanna.tistory.com/entry/%EB%B0%98%EC%82%AC%EB%B2%A1%ED%84%B0

https://gyong0.tistory.com/22

벡터(Vector) 下

◎벡터의 크기

기하학적으로 한 벡터의 크기는 해당 방향이 있는 선분의 길이이다.

벡터의 크기는 이중 수직선으로 표기한다.

Ex ) 벡터 u의 크기는 ||u||이다. 

3차원 벡터의 크기는 피타고라스의 정리를 두 번 적용해 구할 수 있다.

어떻게 ||u||가 저 식이 될까?

벡터를 순수하게 방향을 나타내는 용도로만 사용하면 벡터의 길이는 그다지 중요하지 않을 수 있다.

그런 방향 전용 벡터에서는 벡터의 길이를 정확히 단위 길이인 1로 맞추어 두는 것이 편리하다. 

따라서 벡터의 길이를 단위 길이가 되게 해서 단위 벡터로 만드는 것을 가리켜 벡터의 정규화(normalization)라고 부른다.

벡터의 각 성분을 벡터의 크기로 나누면 벡터가 정규화 된다. 

왜 벡터의 크기로 각 성분을 나누는지 이해가 되지 않는다면 이렇게 생각하면 쉽다. 

벡터의 곱셈에는 두 가지 종류가 있다. 내적과 외적이다.

◎ 내적

스칼라 값을 나타내는 벡터 곱셈의 일종으로 점곱(dot product)라고도 한다.

내적은 결과 값이 뒤에 나올 외적의 결과와 달리 스칼라 값으로 나온다.

u = (u1, u2, u3), v = (v1, v2, v3)라고 가정했을 때 내적은

즉, 대응되는 성분들의 곱들의 합이다.

코사인 법칙을 이용하면 내적의 기하학적 의미를 알아낼 수 있다.

여기서 θ는 벡터 u와 v 사이의 각도이다. 0 ≤ θ ≤ π 사이의 값.

따라서 위의 식은 두 벡터의 내적이 두 벡터 사이의 각도의 코사인을 벡터 크기들로 비례 시킨 것이다. 

특히 u와 v가 둘 다 단위 벡터이면 u, v의 내적은 두 벡터 사이의 각도의 코사인이다. 

1. u·v = 0 이면 u ⊥ v이다. ( = 두 벡터는 직교한다. )

2. u·v > 0 이면 두 벡터 사이의 각도 θ는 90˚보다 작다. ( = 두 벡터는 예각을 이룬다.)

3. u·v < 0 이면 두 벡터 사이의 각도 θ는 90˚보다 크다. ( = 두 벡터는 둔각을 이룬다. )

◎ 외적

결과 값이 스칼라 값을 나타내는 내적과는 달리 외적의 결과는 또 다른 벡터로 가위곱(cross product)라고도 한다. 

외적은 오직 3차원 벡터에 대해서만 정의된다.

두 3차원 벡터 u와 v의 외적을 구하면 u와 v 모두에 직교(수직)인 또 다른 벡터 w가 나온다.

즉, w는 u와 직교이고 v와도 직교이다.

u = (u1, u2, u3), v = (v1, v2, v3)라고 가정했을 때 외적은 다음과 같이 구한다. 

참고 출처

Direct11을 이용한 3D게임프로그래밍 (저; 프랭크 D. 루나, 역; 류광, 출판사; 한빛미디어)