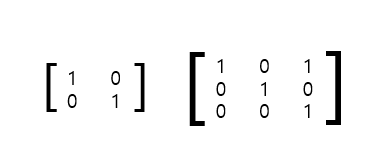오늘의 공부

행렬 下

행렬식, 역행렬, 딸림행렬

◎ 행렬식

행렬식(=determinant)는 정사각행렬에 수를 대응시키는 하나의 함수이다. 이 행렬식은 정사각행렬에서만 정의되는 값으로 행렬의 역행렬 존재여부를 결정한다.

따라서 이 행렬식의 명제,

"정방행렬 A는 오직 det A 가 0이 아닐 때에만 역행렬이 존재한다"

를 이용하면 주어진 행렬의 역을 구할 수 있는지 없는지를 쉽게 판단할 수 있다.

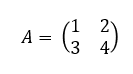
정사각행렬(=정방행렬) A의 행렬식을 흔히 detA라고 표기한다.

A가 2x2의 정방행렬이라고 가정했을 때 역행렬을 표현하는 방법은 다음과 같다. 

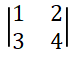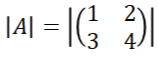행렬식을 구하는 방법은 2x2일 때는 굉장히 간단하다.

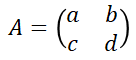
detA = a*d - b*c를 구하면 된다. 

그런데 행렬은 2x2만 있는 것이 아니다. 그 이상의 행렬의 행렬식은 어떻게 구할까?

한 행렬의 행렬식은 재귀적으로 정의된다. 

예를 들어 4x4 행렬의 행렬식은 3x3 행렬의 행렬식을 항으로 해 정의되고 3x3 행렬의 행렬식은 2x2 행렬의 행렬식으로, 2x2는 1x1 행렬의 행렬식으로 정의된다. 이 2x2 행렬의 1x1 행렬식이 바로 위의 ad-bc인 것이다. 

그러면 A가 nxn 행렬이라고 할 때, n > 1 에 대해 A의 행렬식은 다음과 같이 정의된다.

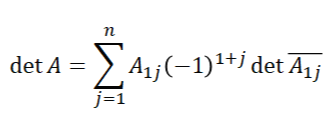
3x3행렬의 소행렬 정의를 이용하면 3x3 행렬의 행렬식의 정의는 아래와 같다.

소행렬?

더보기

n x n 행렬 A가 주어졌을 때, 그 소행렬은 A의 i번째 행과 j번째 열을 삭제한 결과로 생긴 (n - 1) x (n - 1)행렬이다.

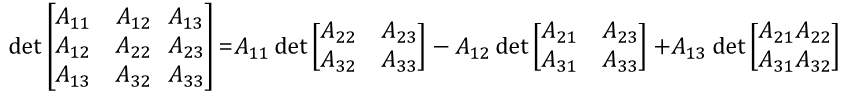
◎ 딸림행렬

딸림행렬은 이해하기 앞서 여인수에 대한 정의가 필요하다.

여인수라는 것은 A가 n x n 행렬이라고 할 때, 아래의 C를 여인수(confactor)라고 부른다.

A의 여인수행렬이란 것은 A의 각 성분에 여인수 C를 해당 ij번째의 위치에 넣어서 만든 행렬을 뜻한다.

그리고 이 여인수행렬의 전치행렬을 A의 딸림행렬(adjoint matrix)라고 부르는 것이다.

◎ 행렬의 역

역행렬은 n차의 정방 행렬 A가 있고 단위행렬을 E라고 할 때 AX = E가 되는 n차의 정방 행렬 X를 뜻한다. 

즉 교환법칙이 성립되지 않는 행렬의 곱셈에서 A에 곱했을 때 단위행렬이 되는 특정 행렬을 말하는 것이다. 

행렬 대수는 나눗셈 연산은 정의하지 않지만 곱셈에 대한 역인 역행렬에 대한 정의는 존재한다. 

행렬 A에 대한 역행렬은 다음과 같이 표현한다.

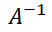
위의 행렬식의 명제를 통해 본것 같이 모든 행렬이 역행렬을 갖는 것은 아니다. 우선 정방행렬(n x n)이어야 하며 행렬식이 0이되어서는 안된다. 

이처럼 역행렬이 있는 행렬을 가역행렬이라고 하고 역행렬이 없는 행렬은 특이행렬이라 부른다. 

역행렬을 구하는 방법은 간단하다. 

행렬의 앞에 앞서 구한 행렬식을 곱해주면 된다. 

참고 자료;

https://namu.wiki/w/%ED%96%89%EB%A0%AC%EC%8B%9D

Direct11을 이용한 3D게임프로그래밍 (저; 프랭크 D. 루나, 역; 류광, 출판사; 한빛미디어)

행렬 上

행렬과 단위행렬, 전치

◎ 행렬

m x n 행렬 M은 m개의 행과 n개의 열로 이루어진 실수들의 정사각 배열이다.

행(row)들의 개수와 열(column)들의 개수를 곱한 것을 행렬의 차원이라고 부르고 행렬을 구성하는 수들을 원소(element) 도는 성분(entry)라고 부른다. 

종종 한 행렬의 행들을 벡터로 간주하는 것이 편할 때가 있다. 예를 들면 A 행렬의 A1* 는 A11, A12, A13으로 하나의 행벡터를 뜻하게 된다. 이 때 *는 하나의 행벡터 전체를 뜻하게 된다.

열벡터도 마찬가지로 A*1는 A11, A21, A31을 뜻하며 여기서의 *는 하나의 열벡터 전체를 뜻한다.

행렬의 한 성분을 지칭할 때에는 그 성분의 행과 열 번호를 이중 아래첨자(색인)로 지정하는 형태의 표기법을 사용한다.

◎ 행렬의 연산

행렬의 상등, 덧셈, 스칼라 곱셈, 뺄셈을 정의해 보면

1. 두 행렬은 오직 대응되는 성분들이 상등일 때에만 상등이다. 따라서, 두 행렬의 상등을 비교하려면 두 행렬의 행 수와 열 수가 동일해야 한다.

2. 두 행렬을 더할 때에는 대응되는 성분들을 더한다. 따라서 행 수와 열 수가 같은 행렬들만 덧셈이 가능하다.

3. 행렬에 하나의 스칼라를 곱할 때는 행렬의 모든 성분에 그 스칼라를 곱한다.

4. 행렬의 뺄셈은 스칼라 곱셈과 행렬 덧셈으로 정의한다. 즉, A - B = A + (-1 x B) = A + (-B)이다.

덧셈과 스칼라 곱셈이 성분별로 이루어지기 때문에 행렬의 덧셈과 스칼라 곱셈도 실수의 덧셈 및 곱셈의 다음과 같은 속성들을 만족한다.

◑ 행렬의 곱셈 

위에서 덧셈은 행렬의 열 수와 행 수가 동일해야 했는데 곱셈은 조금 다르다.

교환법칙이 성립하지 않는 행렬의 곱셈은 앞의 행렬의 열과 뒤에 곱할 행렬의 행의 수가 같아야 한다.

즉, A(앞에 곱하는 행렬)의 행벡터 차원과 B(뒤에 곱하는 행렬)의 열벡터 차원을 일치시켜야 한다. 

만일 A가 m x n 행렬이고 B가 n x p 행렬이면 둘의 곱 AB가 정의된다. 곱 AB는 하나의 m x p 행렬이 된다.

행렬 A와 B를 곱한 결과가 C라고 할 때 C의 ij번째 성분은 A의 i번째 행벡터와 B의 j번째 열벡터의 내적이 된다.

◑ 행렬의 전치

행렬의 전치, 즉 전치행렬은 주어진 행렬의 행들과 열들을 맞바꾼 것을 말한다.

따라서 m x n 행렬의 전치는 n x m 행렬이다. 

행렬 M의 전치행렬은 다음과 같이 표기한다.

◑ 단위행렬

행렬에는 단위행렬이라고 부르는 특별한 행렬이 있다. 주대각 성분, 즉 좌상에서 우하로의 주된 대각선에 있는 성분들만 1이고 나머지는 모두 0인 정방행렬(정사각형 행렬, 즉 열 수와 행 수가 같은 행렬)이다. 

이 단위행렬은 곱셈의 항등원 역할을 한다.

항등원?

즉, 만일 A가 m x n 행렬이고 B가 n x p 행렬 그리고 I 가 n x n 행렬이면 AI = A, IB = B.

그러니까 어떤 행렬에 단위행렬을 곱해도 그 행렬은 변하지 않는다. 

곱할 행렬 M이 정방행렬이라면 단위행렬과의 곱셈은 교환법칙을 만족한다. 

참고 자료;

- Direct11을 이용한 3D게임프로그래밍 (저; 프랭크 D. 루나, 역; 류광, 출판사; 한빛미디어)