삼각함수
각도와 라디안, 그리고 sin cos tan.
◎ 각도와 라디안
라디안은 원주율의 단위이다. 호의 길의로 각도를 나타내기 때문에 호도법이라고도 한다.
xy 좌표계에서 한바퀴를 돌아 제자리로 돌아오는 것은 360˚이다. 그리고 이에 해당하는 라디안 단위의 크기는 2πr이다.
우리는 일상생활에서 각도를 많이 써서 각도가 더 익숙하다.
그러나 라디안을 이용하면 호의 길이와 각도를 구하기가 더 편리하고 깔끔하게 알아보기 쉽기 때문에 이러한 계산이 필요한 곳에서는 호도법을 이용한다.

위의 그림같이 원의 반지름과 길이가 같은 호가 대하는 중심각의 크기는 1라디안이다.
◑ 도→ 라디안
| 도 단위의 각 * (π/180) |
모든 C++ 삼각함수 라이브러리, sin()이나 cos(), tan() 등과 같은 것들은 라디안을 사용하고 삼각함수의 역함수 라이브러리의 리턴값 역시 라디안 단위이다.
이런 것들은 미리 PI값을 #define 지시문으로 간편하게 변환을 할 수 있게 매크로로 정의해 놓는 것이 좋다.
◎ 삼각함수 (sin, cos, tan)
모든 삼각함수는 직각삼각형에 대해 정의된다.
그리고 그 직각삼각형을 통해 sin, cos, tan를 정의할 수 있다.
삼각함수는 직각 삼각형에서 빗변, 높이, 밑변 사이의 비율을 나타내 흔히 삼각비라고도 한다.
위와 같은 삼각형이 있을 때

| sin Θ | cos Θ | tan Θ | |
| 30˚ |  |
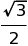 |
 |
| 45˚ |  |
 |
 |
| 60˚ | 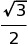 |
 |
 |
 |
 |
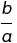 |
sin의 역함수는 csc(코시컨트), cos의 역함수는 sec(시컨트), tan의 역함수는 cot(코탄젠트)로 정의된다.
| csc Θ | sec Θ | cot Θ |
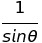 |
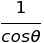 |
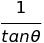 |
이런 역함수들은 사인, 코사인, 탄젠트가 포함된 분수를 없애서 식을 간단하게 만들고자할 때나 여러 방면에서 활용이 가능하다.
◎ 삼각함수의 합차공식
삼각함수의 합차공식은 벡터의 회전을 구할 때 사용된다.

참고 자료;
https://ko.wikipedia.org/wiki/%EB%9D%BC%EB%94%94%EC%95%88
라디안 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 라디안(영어: radian)은 각의 크기를 재는 SI 단위이다. 호도(弧度)라고도 하며, 기호는 rad이다. 단위원의 중심각의 라디안 값은 그 각이 대하는 호의 길이와 같다. 1라디안은 약 57.3도이다. 라디안은 입체각의 단위인 스테라디안과 함께 SI 보조 단위에 속했으나, 1995년에 SI 보조 단위가 폐지되면서 SI 유도 단위가 되었다. 라디안의 표기는 rad 기호가 가장 흔하며, 이는 자주 생략된다. 간혹 c(위첨
ko.wikipedia.org
게임 프로그래머를 위한 기초 수학과 물리 (저; 웬디 스타일러, 더스틴 클링맨, 카베 카히리쯔 , 역 ; 엄윤섭 , 출판사 ; 제우미디어 )
'GameProgramming > 게임수학 & 물리' 카테고리의 다른 글
| [게임수학] 행렬 上 (연산, 단위행렬, 전치행렬) (0) | 2020.02.12 |
|---|---|
| [게임 수학] 포물선과 원 충돌체크 (0) | 2020.01.21 |
| [게임 수학] 두 점 사이의 거리 구하기 (0) | 2020.01.21 |
| [게임수학] 벡터(Vector) 下 (0) | 2020.01.10 |
| [게임수학] 벡터(Vector) 上 (0) | 2020.01.09 |