기수 정렬과 계수 정렬
최악의 경우에도 비교 정렬들보다 빠른 정렬 알고리즘
최악의 경우 정렬 시간이 O(nlogn)보다 빠를 수는 없을까? 원소 두 개를 비교함에 의해 정렬하는 비교정렬은 최악의경우 수행 시간이 O(nlogn)보다 빨라질 수는 없다.
그런데 입력 원소들이 특수한 성질을 만족하는 경우 O(nlogn)의 한계를 극복할 수 있는 정렬 알고리즘들이 존재한다.
기수 정렬과 계수 정렬이다.
◎ 기수 정렬
기수 정렬은 문자열의 정렬에도 사용되는 방법이다.
입력이 모두 k 이하의 자리수를 가진 자연수인 특수한 경우에(자연수가 아닌 제한된 종류를 가진 알파벳 등도 해당 된다) 사용할 수 있는 방법으로 O(n) 시간이 소요되는 정렬 알고리즘이다.
작동의 순서는 다음과 같다.
1. 우선 가장 낮은 자리수만 가지고 모든 수를 재배열(정렬)한다.
2. 그런 다음 가장 낮은 자리수는 잊어버린다.
3. 그 다음은 앞과 같은 방법으로 더이상 자리수가 안 남을 때까지 반복한다.
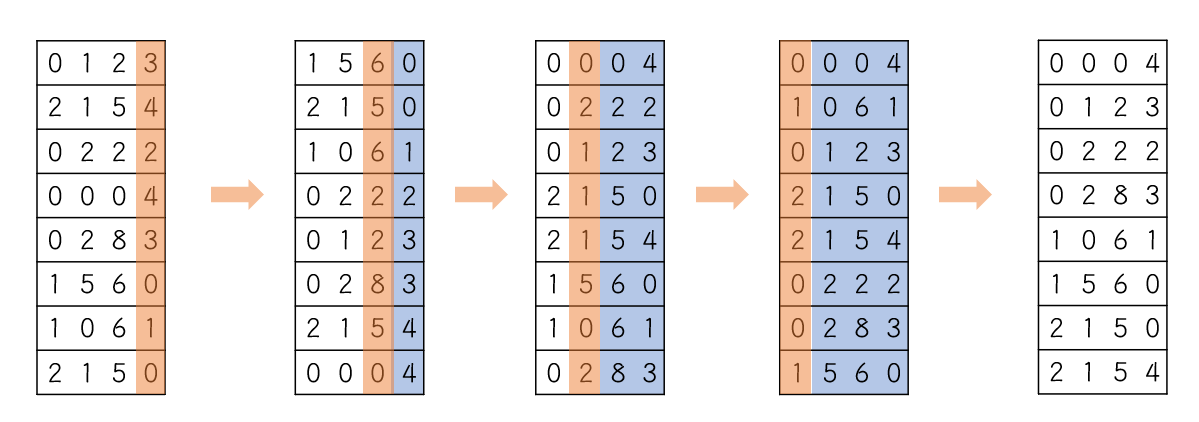
구현 방법은 우선 0부터 9까지의 버킷을 만든다.
그 후에 1의 자리를 비교한다. 0123같은 경우에는 3번 버킷에, 2154는 4번 버킷에 들어간다.
이 때 버킷의 각 번호는 FIFO의 구조를 가진 queue이다.
그 후 0번 버킷부터 9번버킷까지 각 버킷에 저장된 숫자들을 뺀다.
다음으로는 10의 자리를 비교해서 위와 같은 과정을 거친다.
이 과정을 거치게 되면 마지막에는 정렬된 배열을 갖게 된다.
만약 첫 문자에서 정렬을 시작하게 된다면 MSD 기수 정렬, 마지막 문자에서부터 정렬을 시작하게 되면 LSD 기수 정렬이라고 한다.
이 알고리즘은 "안정성을 유지하면서 정렬된다"
이 말은 같은 값을 가진 아이템들은 정렬 후에도 원래의 순서가 유지되는 성질을 가진 정렬을 일컫는 말이다.
즉, 값이 같은 원소끼리는 정렬 후에 원래의 순서가 바뀌지 않는 성질을 말한다.
◎ 계수 정렬
계수 정렬은 정렬하고자 하는 원소들의 값이 O(n)을 넘지 않는 경우에 사용할 수 있다.
기본적인 특성은 버켓 정렬과 유사하지만 중복되는 키 값의 누적된 횟수를 구해서 그것을 인덱스로 삼는다.
작동의 순서는 다음과 같다.
ex) 0,3,2,1,0,0,2,3,1,1,1 을 정렬한다고 할 때
1. 우선 각 배열의 원소를 훑어보고 각 키의 값이 몇 번씩 있는지 빈도수를 구한다.
| 숫자 | 0 | 1 | 2 | 3 |
| 빈도 수 | 3 | 4 | 2 | 2 |
2. 각 키의 등장 횟수를 누적 합으로 바꿔준다.
| 숫자 | 0 | 1 | 2 | 3 |
| 누적 합 | 3(3) | 7(3+4) | 9(3+4+2) | 11(3+4+2+2) |
3. 위의 누적합은 새로 할당할 공간의 최댓값이 된다.
즉 숫자 0의 인덱스는 1과 3의 사이이다.
0이 3번 반복뒤니까 0을 3번째 인덱스에 넣은 후에 0의 누적 합을 2로 줄인다. 그 후 3의 누적 합은 11이므로 3을 11번 인덱스에 집어 넣고 3의 누적 합을 10으로 줄여준다.
4. 2의 경우에도 마찬가지로 빈도 수는 2, 누적합은 9이므로 9에 넣고 누적합을 8로 줄여준다.
이런 식으로 반복하며 정렬해야 하는 모든 값의 인덱스를 정해줄 수 있다.
계수정렬도 마찬가지로 안정 정렬이며 다른 정렬들 보다 시간 복잡도에서 좋은 효율을 보이는 이유는 키 값의 비교를 하지 않고 (비교정렬) 바로 자기 자리를 찾기 때문이다.
참고 자료;
쉽게 배우는 알고리즘 - 관계 중심의 사고법 (출판사; 한빛 아카데미 / 저; 문병로)
'알고리즘 & 자료구조 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 이분(이진)탐색 (Binary Search) (0) | 2020.10.21 |
|---|---|
| [알고리즘] 순열/조합 구현 (C++) (1) | 2020.09.24 |